机器学习-白板推导 2 高斯分布
机器学习-白板推导 2 高斯分布
1. 从概率密度函数看高斯分布
高斯分布的pdf:
后面式子是二次型,其中,是维随机变量。
通常来说 是半正定的(对称的),这里假设其是正定的,, 因为是自变量,所以这个只跟有关。这是个数,也叫马氏距离 ( 与 之间的距离)。
马氏距离
当时,就是欧氏距离。
在高斯分布中,$(X-\mu)^T\Sigma^{-1}(X-\mu)$的计算结果是一个数,这个数被称为马氏距离。设,。那么和之间的马氏距离为,
显然,当时,马氏距离等于欧式距离。
对标准差进行特征分解
由于$\Sigma$为实对称矩阵,那么可以对$\Sigma$进行特征分解,那么有,并且,所以,,并且。
而的求解过程如下所示:
代入可以解得:
那么,
令,这是一个典型的投影算法,其中是特征值为的特征向量,那么
当时, 有:
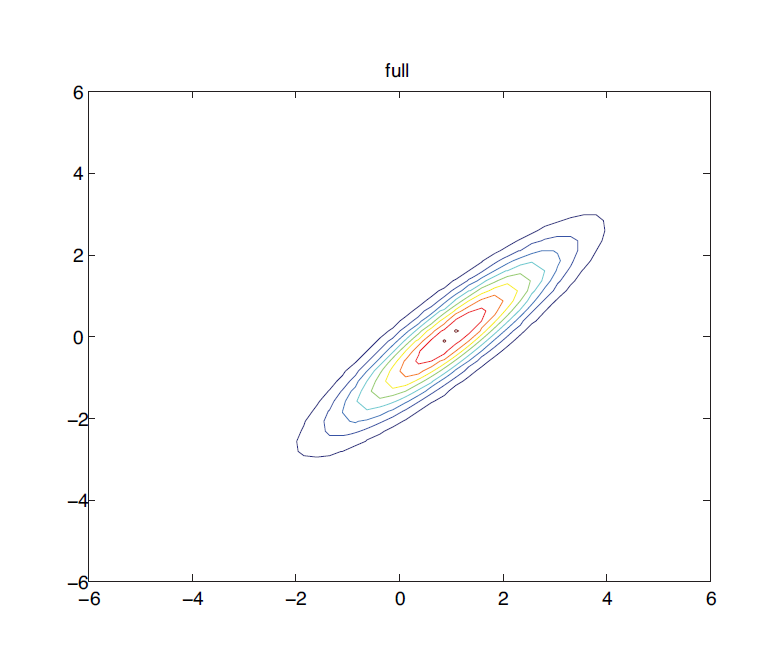
每当 取不同值,椭圆就相当于对这一高度的等高线,也对应一个固定的概率值,若) (常量)时,图中椭圆便是一个圆。
具体如下面两图所示,高度是概率值的话, ,就是去不同概率值时切出一个个椭圆。图出自 [Machine Learning: a Probabilistic Perspective P48 Joint probability distributions ]

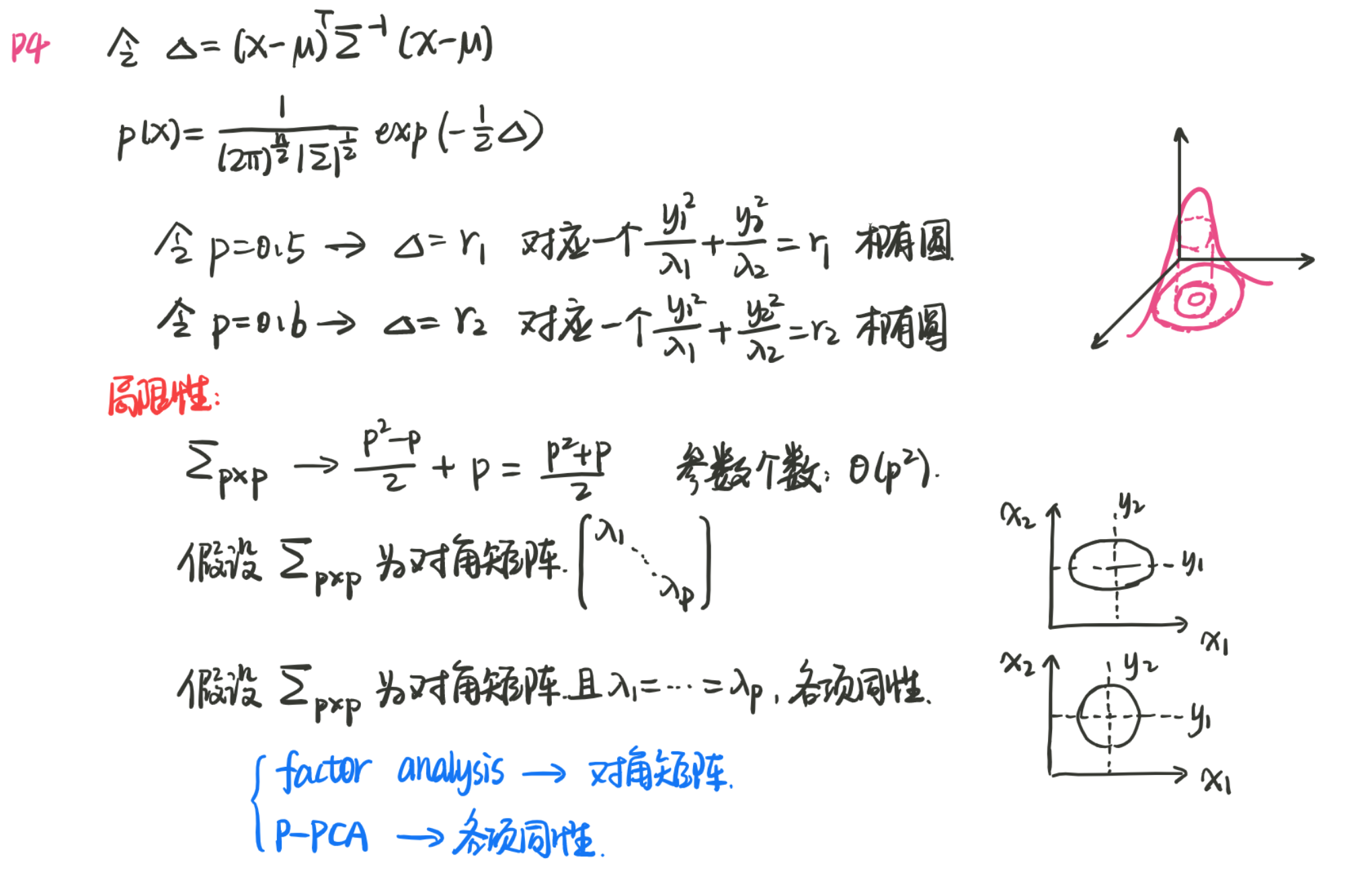
2. 高斯分布的局限性
来自 数学基础.pdf
3. 已知联合概率求边缘概率及条件概率
高斯分布的一个定理:
证明:
假定多元高斯分布:
其中,
若已知联合概率密度求条件概率密度和边缘概率密度,可描述为已知:(就是将变量x分为两部分, )
求:和
而
就是这种形式,按照式3可以有:
同样地, .
下面是最关键的3个构造式,(没有为什么,就是这样构造能解决问题,不然用PRML上配方法)。
式5中最后一个式子叫舒尔补,补充下 舒尔补:
假设有分别属于以及’的随机列向量,并且中的向量对 具有多维正态分布,其方差矩阵是对称的正定矩阵
那么’’X’’在’’Y’’给定时的[[条件方差]]是矩阵’’C’’在’’V’’中的舒尔补:
由式5中第一个式子得到:
同样按照式3有:
同样由式5中第一个式子得到 , 在求条件概率时,对于可以看做是已知,因此:
同理可得:
即:。同理可得
4. 求联合概率分布
上面是已知联合概率分布求条件概率分布和边缘概率分布。
而下面内容是:
已知:
- , 这里 是精度矩阵,就是协方差矩阵的导数 ,详见PRML中文版P68.只是为了计算,写成这样。
求:
证明:
假设, 这里。
求解
所以
求解
先引入一个变量
那么可得:
这里:
5. Jensen’s Inequality
Jensen’s Inequality 是在给定是凸函数的条件下,过凸函数上任意两点所作割线一定在两点函数图像上方,即对于, 有:
如下图所示,
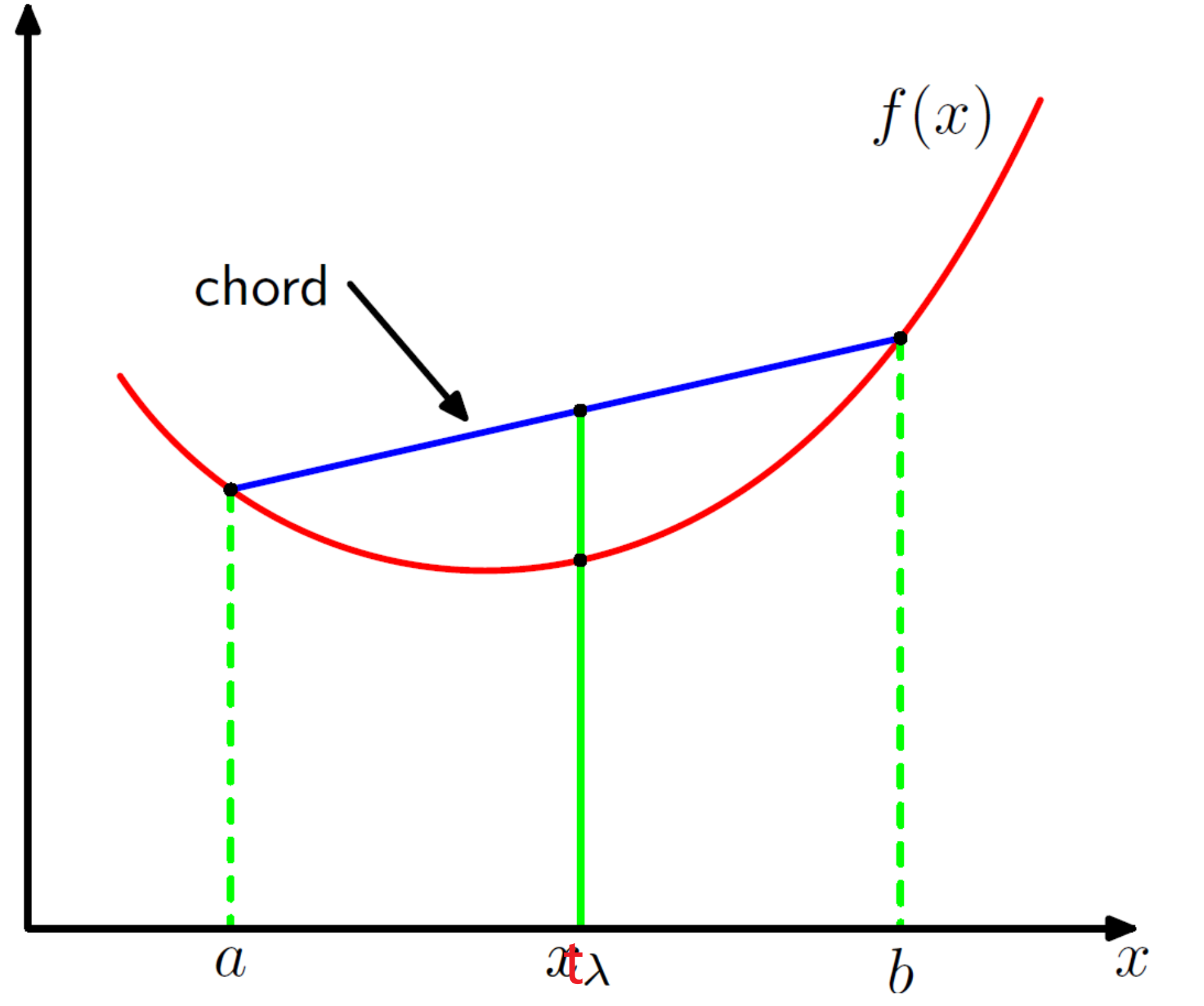
在概率论中,其中是该点的切线,设其为有
Inference
[1] 特征值分解
[2] 高斯分布
[3] 高斯分布|机器学习推导系列(二)



